Min vän matteläraren har ett skarpt mediekritiskt öga (tack för bilden!). Men då vi journalister går loss och försöker räkna är det ju ofta som att släppa in en elefant i en porslinsaffär. Det behövs inget skarpt öga. Vem som helst som känner en elefant (eller journalist) fattar hur det kommer att gå.
Och resultatet kan det minsta skolbarn tolka.
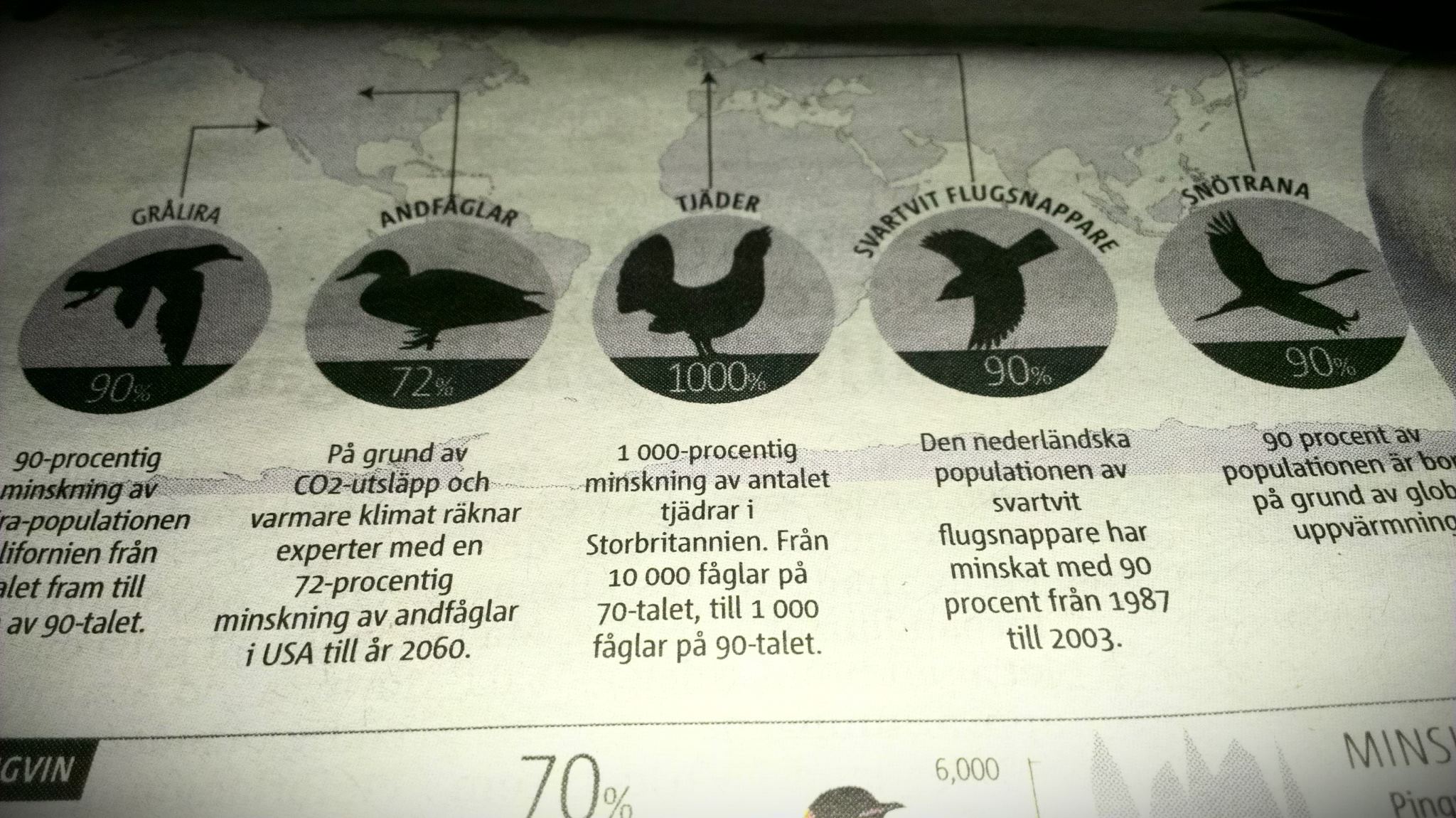
Ofta blir det ändå rätt. Men de gångerna blir det ofta rätt för att reportern haft vett att fråga någon som kan räkna – inte tack vare egna meriter.
Det tokiga i den här tidningen är tjädrarna. Vi tar det enkelt och steg för steg. Vi hade 10.000 fåglar från början. De minskade till 1.000. Nu kan vi tänka på två sätt:
Antingen kan vi tänka att det nu återstår 1.000 av de 10.000. 1.000 av 10.000 är helt uppenbart 10 procent. Vi vet alltså att återstoden av fåglarna är 10 procent. Vi kan säga att ”bara 10 procent av tjädrarna i Storbritannien finns kvar” (och så måste man förstås sätta in det i något slags tidskontext, så vi vet vad vi har att utgå ifrån). Hur som helst: om återstoden är 10 procent – vad är då de andra 90 procenten upp till 100 procent? Det är det som är minskningen. ”90 procent av tjädrarna försvann.”
Det andra sättet man kan tänka på är att om det i dag återstår 1.000 av de ursprungliga 10.000 tjädrarna, så är alltså minskningen i antal 9.000. Det råder det knappast några tvivel om. Nu vet vi alltså hur stor minskningen är i antal. Men hur stor är den i procent? Vi dividerar även nu delen med det hela, och får 9.000 / 10.000 = 0,9 = 90 procent. Och de 10 procent som återstår upp till 100 procent, är, som vi konstaterade då vi resonerade från andra hållet, förstås återstoden.
100 procent är ju helheten. 1.000 procent är alltså mer än helheten. Om vi drar bort mer än vad vi har, så hamnar vi alltså på minus. Säg till om du hittar några minustjädrar i Storbritannien. Då jävlar har du ett scoop!